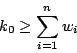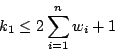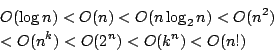2007年5月22日星期二

未來數學家的挑戰【七、結論+註釋】

七、結論

現在你明白二十世紀的大難題了，P=NP？用簡單的語言說，就是是否能找到一個只呈方次增加的方法去解決旅行、包裝、舞會等問題。平凡的問題，期待您不平凡的解答。


1. Gorey, M.R. and Johnson, D.S.《Computers and Intractability-A Guide to Theory of NP-Completeness》, 1979, Freeman and Company.

2. Pearl, J.《Hearistics-Intelligent Search Strategies for Computer Problem Solving》,1984, Addsion-Wesley.

3. Cook, S.A.〈The complexity of theorm-proving procedure〉, Proc. 3rd Ann. ACM Symp. on Theory of Computing, 1971, 151-158.

4. Jonhson, D.S. et. al.〈Worst case performance bounds for simple one-dimensional packing algorithms〉, SIAM J. Comp., 1974, 299-325.

5. Rosenkrantz, D.J. et. tl.〈An analysis of several heurishics for the traveling salesman problem〉, SIAM J. Comp., 1977, 563-581.

6. Sahin,S. and Gonzalez,〈P-complete approximation problems〉, J. ACM, 1976, 555-565.

7. Stockmeyer, L.J. and Meyer, P.R.〈Word problems requiring exponential time〉, Proc. 5th. Ann. ACM Symp. on Theory of Computing, 1973, 1-9.

8. Robertson,E. and Munro, I. 〈NP-completeness, puzzles, and games〉 Utilifas Math., 1978, 99-116.
註釋

...1
排序 (Sorting) 的方法很多，但都不能低於 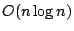$O(n\log{n})$，讀者可在一般 Database 的書中找到有關 Sorting 的法則。
...2
又稱呈多項式上升，但因一個 n 的多項式之大小，在 n 很大時都為第一項所支配，故可寫成 O(nk)。
...3
並不失去一般性，即若距離不是正整數也可以把它們化成正整數。
...4
在古克的原文中，並沒有 NP-complete, NP-hard 之明確定義。但是由於他的論文，使這種分法顯得很自然。 不過 NP-hard 之定義仍因人而異，不一定同於本文。
...5
本文中之解決，均指一個 O(nk) 計量算的解法。
...6
與情報人員之單線作用相同。一個諜報人員只知道他的頂頭上司及他的第一線下層下屬，其餘的人他都不知道。
...7
A,B,C 表任三城，而 d(A,B),d(B,C),d(C,A) 分別表示 A,B; B,C; C,A 城之距離，則 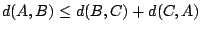$d(A,B)\leq d(B,C)+d(C,A)$ 稱為三角不等式。
...8
指 19×19 之棋盤，許多計算機學家都是圍棋高手，中國的算盤與圍棋，好像包含了計算機的開始與終極。

发帖者 Alpha 时间： 16:27 0 评论 A A A A

标签： ,

未來數學家的挑戰【六、NP-hardness 與圍棋】

六、NP-hardness 與圍棋

不是所有的難題都可歸結為 NP 問題，像下得一手絕對好的圍棋現在目前的推測是比所有 NP 問題還要難的計算問題，即 NP-hard 問題，NP-hard 問題的定義如下：



定義： 若 x 為一 NP-hard 問題，則若 NP $\neq P$，則 $x\not\in P$。

也就是說，即使 P=NP，x 還不一定屬於 P，但 $P\neq$NP, 則 x 絕不比 NP 的問題容易。在第三節中的問題1、3不一定是 NP 問題，但若能以 O(nk) 的計算量解決它們，則比較容易的問題2與4也可以 O(nk) 解決， 故若問題1、3$\in P$ 則問題2、4$\in P$，又因2、4是 NP-complete，即推出 NP=P。 這與 NP-hard 之定義相合，故問題1、3均為 NP-hard 問題。 同理問題5也屬於 NP-hard，不過這些 NP-hard 似乎比 NP 難不了多少，但下棋問題可能比 NP 問題要難得多，圍棋問題可以作如下觀。


問題11.（圍棋問題）
以平常的圍棋規則在一個 n x n 的棋盤上下，給定一個殘局（下了二個子就可以算殘局），首先，是否可以確定黑子在最好的下法之下，一定會贏？

這個問題不能用一般的方法證明它是不是為 NP。 因為目前沒有人能猜一個必勝的下法且在 O(np) 時內證明它是對的，因為它與對方如何應付有關，而敵方的應付又與他對你以後的下法的推測有關，如此往下走，首先發生困難的是記憶上亮了紅燈，即所需要的記憶可能呈方次以上的進展。

因每一個記憶至少要用（來計算）一次，否則這個記憶就不如不要，因此一個問題的記憶若呈指數上升，則其計算量亦非呈指數似的上升不可，但若某問題只需要方次上升的記憶，即不能保證它只需要方次上升的計算量。

因此計算機學家定義三個新的集合：


PSPACE={x：x 只需要方次上升的記憶 }
註：x 均指問題。


PSPACE-complete：

若 $x\in$ PSPACE,

又 $x\in$ PSPACE-complete,

且 $x\in P$,

則 P= PSPACE。


PSPACE-hard：

若 $x\in$ PSPACE-hard,

且 $x\in P$,

則 P= PSPACE。

注意在上式中 PSPACE-complete $\subset$ PSPACE，即 PSPACE-complete 是 PSPACE 中的難題，但 PSPACE-hard 不一定屬於 PSPACE。 Stockmeyer and Meyer 在1937年證明了一個與古克相似的定理。

若令 $\exists x$ 表示存在一個 x，$\forall x$ 表對所有的 x，Q 表 $\exists$， $\forall$ 中的一個，x 為布氏變數0與1，則我們稱 f(Q1 x1,Q2 x2,…,Qn xn) 為一量化布氏公式。若 f 有可能為1，則 f 稱之為可滿足，例如把第四節中之(1)式改寫成

\begin{displaymath} f(\forall u_1,\exists u_2,\forall u_3)\\ =((\forall u_1)\cd... ...ts u_2)\cdot \\ (\exists u_2)+\forall u_3)\cdot(\forall u_3)) \end{displaymath}

則上式不可能滿足，因對 $\forall u_3$（u3 為 0 或 1）而言，f 不全是1。

Stockmeyer 與 Meyer 之定理為：


定理：
檢定一個量化布氏公式為可滿足是一個 PSPACE-complete 問題。

當我們下棋面對著一盤殘局沉思的時候，我們的要求是

對我是否存在一著必勝棋可以對付
敵人任何一著應付棋
此後我是否存在一著必勝棋可以對付
敵人任何一著應付棋
……
我是否存在一著必勝棋可以對付
敵人任何一著棋
我贏了

因此這完全是 $\exists$,$\forall$,$\exists$,$\forall$,… 之交替作用與Stockmeyer 與 Meyer 定理之關係至為密切， Robertson 與 Munro 在1918年證得圍棋是一種 PSPACE-hard 的問題， 目前有人計算到圍棋 8 必勝法之記憶計算量在 10600 以上，不論人腦或電腦的記憶絕少不了一個原子， 而現今所知的宇宙原子數約只有 1075。棋之道，大矣哉！要做一個下圍棋必勝的機器人是談何容易！

发帖者 Alpha 时间： 16:26 17 评论 A A A A

标签： ,

未來數學家的挑戰【五、NP-complete 問題之近似解】

http://episte.math.ntu.edu.tw/articles/mm/mm_10_2_04/page5.html
五、NP-complete 問題之近似解

NP-complete 問題既找不到可行的解法，而很大部分的 NP-complete 問題都在計算機語言，程式，電路設計，統計學，程式作業上有大用，因此只好退而求其次找一個可行的近似解。很可惜的是，所有的 NP-complete 問題雖在 NP 的層次上相聯，在近似解上往往各需不同的解法，這些解法多從直觀而來，我們在此舉二個例子。


例1
在第三節問題5，包裝問題中，若採取「能裝就裝」法，即現有的盒子若可以裝得下，就不用新盒子，則此法所需用之盒子數 k1 與最可能少的盒子數 k0 滿足 $k_1\leq 2k_0+1$。

證明
今令 n 個物品之重為 w1,w2,…,wn 公斤，因每個盒子只可以裝1公斤，故
\begin{displaymath} k_0\geq \sum_{i=1}^{n}{w_i} \end{displaymath}

另一方面，「能裝就裝」法不可能有兩個以上的盒子同時少於 $\frac{1}{2}$ 公斤，故
\begin{displaymath} k_1\leq 2\sum_{i=1}^{n}{w_i}+1 \end{displaymath}

本例得證。

這個問題的結果是說，我們大約可以用「能裝就裝」法做得最好情形的一半好。 經過較複雜的證明，Johnson 在1974年證得，當 n 很大時，

(i)
$k_1\leq \frac{17}{10} k_0+2$，且存在一種情形能產生。

(ii)
$k_1\geq \frac{17}{10} (k_0-1)$

也就是用「能裝就裝」法不會壞到 70% 以上，但可以壞到多用了 70% 的盒子。

售貨員旅行問題的一個直觀走法是先訪問最近那個尚未訪問過的城，稱為「先訪近城」法，以圖1為例，其走法為

\begin{displaymath} A\rightarrow G\rightarrow C\rightarrow B\rightarrow D\rightarrow F\rightarrow E\rightarrow A \end{displaymath}

Rosenkrantz 等在1977年證明這並不是一個很理想的走法，他們證出若各城間的距離滿足三角不等式 7 ，則「先訪近城」法所走之總程 D1 與最短路徑 D0 之關係為
\begin{displaymath} D_1\leq \frac{1}{2}([\log_2n]+1)D_0 \end{displaymath}

且當 n 很大時，可以有一種情形使得
\begin{displaymath} D_1\geq \frac{1}{3}(\log_2n+\frac{4}{3})D_0 \end{displaymath}

上式中之 [x] 表示大於 x 之最小整數，例如 [5]=5, [2.5]=3。 因 $\log_2n$ 當 n 大時可以很大，故 D1 可與 D0 相差非常之大，但在同一篇論文之中，Rosenkrantz 等證明另一種複雜的「直觀」走法可以達到 $D_1\leq 2D_0$ 之地步。

在上面的定理中，三角不等式的條件很重要，若城之距離無此關係存在時，Sahni 與Gonzalez 在1976年證得：若 $P\neq$NP，則不可能存在一個有限的 m，及一個 O(nk) 計算量的走法，能使其全程長 D1 在任何 n 時滿足

\begin{displaymath} D_1\leq mD_0 \end{displaymath}

即上式中 m 非等於無限大不可，亦即所有 O(nk) 的做法都不很好。

发帖者 Alpha 时间： 16:25 13 评论 A A A A

标签： ,

未來數學家的挑戰【四、古克定律與 NP-completeness】

四、古克定律與 NP-completeness

古克定律的證明很難，就是瞭解它也不容易，我們將從幾個角度來看這個問題，試著去暸解它。它的主要結果是把前節那類問題大部歸於一個較易證明的集合，稱之為 NP，而在 NP 中找到一批互依的問題稱之為 NP-complete 類並得到下面的結果。


1. 若有一個 NP-complete 問題可以用 O(nk) 計算量來解決， 則全體的 NP 問題都可以用 O(nk) 之計算量來解決，即

1' 若有一個 $x\in$ NP-complete且 $x\in P$，則 P=NP。

又換句話說，NP-complete 是 NP 中的難題，NP-complete 解決了 5 ， NP 就解決了。但若有一個屬於 NP 而不屬於 NP-complete 的問題解決了，則其他的 NP 問題不一定可以解決。

什麼叫做 NP？NP 是英文 nondeterministic polynomial 的縮寫，意思就是非確定性的多項式時間。要暸解這個字。我們先看一看普通計算機的作用。

現在已知用一個計算機，要解決售貨員旅行問題非常困難，但若我們有許多計算機同時用，是否可以快到把原問題在 O(nk) 時間內解決？「許多」，不是一、二，多一二個是於事無補的，多百個千個仍是杯水車薪，不能有很大的作用，因為就是一千個機子可以分開做，也最多只能快一千倍，在第一節內已說過，幫助不大。 因此計算機學家先放眼望去，乾脆允許你可以無限的增加機器。 現在我們要注意的是並不是有了無限多的機器所有的問題就可以立刻解決了，因有的問題有先後次序，例如在算下式的時候

[(a1+a2)a3+a4]a5+a6

除非換個形式，否則必須一步一步的解括弧，機子多了並不能加快計算的速度，而且機子多了，其間之聯絡千變萬化，一個機子要應付千千萬萬別的機子送來的信號也疲於奔命了。 因此我們只假定所有的機子都只承上啟下，單線作業，不作任何橫向聯絡 6 ，也就是說，機器1可以把它的結果傳給它下面的機子，像 a1,a2,…,an 而每一個機子又可以把它們的結果傳給自己的子機， 但在 a1,a2,…,an 之間不互相聯絡。 以售貨員旅行問題為例，若有20個城，第一個機子開始，叫下面19個機子各取一個不同的城及計算與 A 距離， 而這個19個機子又將它所求得的距離交給自己的18個子機令它們取一個與自己不同的城加上距離，如此往下，在第十次時， 第十階段的機子把它已取9城及總距離告訴下一個機子，叫他們再取一與已取之城不同之城加上距離，如此一直做到第19次， 所有路線的距離都有了，在時間上求得所有的距離是 O(n)（但用了 19! 個計算機）， 古克定義凡可以在 O(nk) 時間內用無限多計算機解決的問題為一 NP 問題。

現在要記住的是由於無橫向連絡，在所有路徑的距離都有了之後，並沒有解決售貨員問題（甲），因為不知誰是最短（若加以比較以求最短距離，則要 O(n!) 個比較），因此我們不能說售貨員旅行問題（甲）是一個 NP 問題。 但上節問題2，售貨員旅行問題乙，任何一個單線都可以知道它的總距離是否不大於 B， 因此每單線都有一個「Yes」或「No」的答案。 只要有一個「Yes」的答案，我們即知道本問題已解決，故問題二是一個 NP 問題。在單線作業中，每個機子可以作三件事。

  1. 目前答案不明確，大家各自作業。

  2. 某線已找到答案，立刻叫停，大家停止作業，解題完畢。

  3. 此路不通，本線不再作業，但不叫停，別線仍然作業。

從上項作用，很容易看出找出答案的計算時間即某線叫停的時間，亦即任何一個有「Yes」答案線中計算量之總和， 也就是說找到答案「捷徑」上所需的時間。易言之，在一非確定性計算機系統下，其子機像有「猜測」到捷徑的功能。 若在任何計算步驟中，某人猜了一個答案，而計算機可以在 O(nk) 時間內回答「Yes」或「No」，這個問題即是一個 NP 問題。 再以售貨員旅行（甲）及圖1為例，若你猜一個路徑

\begin{displaymath}A\rightarrow B\rightarrow C\rightarrow D\rightarrow E\rightarrow F\rightarrow G\rightarrow A\end{displaymath}

我們無法知道此路是否最短，但在(B)問題中，一個「Yes」或「No」的結果只要7個加法就可以回答了。 因此根據新的定義，問題2是一個 NP 問題。

由這兩個定義，讀者不難看出問題2,4,6,7,8,9（乙）與10皆為 NP 問題，特別是問題9之（甲），（乙）， 其實是一樣的問題，但如果你猜二個 m,n，立刻就可知道 a 是否是 mn。

古克定理的關鍵在證明若一種叫滿足問題 (Satisfactability Problem) 的例子屬於 P， 則所有 NP 問題均屬於 P（即此問題屬於 NP-complete）， 令 $\cdot$,+,-（且，或，反）表三個基本的邏輯運算（即對0與1邏輯符號而言，$\bar{0}=1$,$\bar{1}=0$,除了1+1=1之外，+，$\cdot$ 與一般代數之加乘相同）。 令 f 為一個含有 n 個邏輯變數 (u1,u2,…,un) 的函數。 假如我們可以找到一組 u1,u2,…,un，使得 f(u1,u2,…,un) = 1，則 f(u1,u2,…,un) 稱為可滿足。 例如

\begin{displaymath} f(u_1,u_2,u_3)=(u_1\cdot(\bar{u_1}+u_2)\cdot u_2+u_3)\cdot u_3 \eqno{(1)} \end{displaymath}

為一可滿足函數，取 u1=u2=u3=1 即可，但
\begin{displaymath} f(u_1,u_2,u_3)=(\bar{u_1}\cdot u_1+u_2\cdot \bar{u_2})(u_1+u_2+u_3) \eqno{(2)} \end{displaymath}

永為 0，故此 f 為不可滿足。

直覺上，這類問題除了將 u1, u2,…,un 一個一個以 0,1 代入檢查 2n 次之外，顯無捷徑可循，古克1971年之論文即證明這是一切 NP 問題之母。


古克定理：
滿足問題為 NP-complete。

現在已可證明在前節中之問題，除了問題1,3,5,9 之外，全是 NP-complete 問題。

发帖者 Alpha 时间： 16:22 0 评论 A A A A

标签： ,

未來數學家的挑戰【三、P 之外？】

三、P 之外？

本節之題目有點不平常，我們的目的是提醒讀者本文中常用之英文大寫的 P 是一個凡能用 O(nk) 計算量解決之問題之集合。而 P 之外加一個問號係指到目前為止，我們尚不知道 P 之外是否是一個空集合。

到目前為止，除了售貨員旅行問題之外，已經有上百有趣或有用的問題，無法用 O(nk) 的計算量來解決，我們在此列舉幾個例子。

問題1：售貨員旅行問題（甲）
即第一節所述之問題，不再重複，不過假定所有距離均為正整數 3 。

問題2：售貨員旅行問題（乙）
與第一題之條件相同，但現在有一個給定之正整數 B，問題是是否存在一條路徑其總距離不大於 B。（問題1與問題2在表面上相似，但在以後的理論上有很大的不同）

問題3：背袋問題（甲）
有物體 n 個，各重 w1,w2,…,wn，今欲將它們分為二袋，試問如何分法可使兩袋之重量最為接近。（不妨假定 wi 皆為正整數，這並未失去一般性。)

問題4：背袋問題（乙）
如上題，並給定一正整數 B，試問可否選出若干 wi，使其和

\begin{displaymath} S \leq \sum_{i=1}^{n} \frac{w_i}{2} \mbox{{\fontfamily{cwM0}\fontseries{m}\selectfont \char 47}} S \geq B \end{displaymath}

問題5：包裝問題
有 n 個各別重量小於 1 公斤的物品及足夠可以裝 1 公斤東西的盒子，今將物品裝於盒子之中，多個物品可裝於一盒，但任何一盒不得重於 1 公斤，試求最小的盒子數。

問題6：舞伴問題
今有 n 個男孩子與 n 個女孩子參加舞會，每個男孩與女孩均交給主持一個名單，寫上他（她）中意的舞伴（至少一人，但可以多於一人）。試問主持人在收到名單後，是否可以分成 n 對，使每人均得到他（她）所喜歡的舞伴。

問題7：庫存問題
某倉庫有 D 個存倉，排成一列，今有 n 批貨物，各可佔有一個或多個存倉，並已知各批物品存入與提出之日期。試問可否將各貨物存入庫裏不發生存倉不夠的困難且同一批貨物若需一個以上存倉時，其存倉必須相鄰。

問題8：
已知 a,b,n 三正整數，問是否存在一小於 n 位之正整數使得

\begin{displaymath} x^2 \equiv a \pmod{b} \end{displaymath}

問題9：

（甲） 給定一 n 位正整數 a，試問其是否為質數？
（乙） 給定一 n 位正整數 a，試問是否存在 m,n >1 且 a=mn？

問題10：分叢問題
已知空間 n 個點，並假定各點之間之距離為正整數，又給定兩正整數 K 與 B，問是否可將此 n 點分成小於 K 個不重合的子集，使得在同一子集內之任意二點距離均不大於 B？

現在可以看出這類問題的一般結構了。很顯然的，有些是極有用的問題，而有些可以轉換成有用的問題。例如舞伴問題，若把男孩與女孩換成工人與工頭，或醫生與病人就有大用了。這些問題到目前沒有一個可以證明是屬於 P 的，大家都猜測它們可能在 P 之外，即其計算量是呈指數增加的。

在60年代，已有些人把某些問題歸於一類了，即是幾個問題是互依的，若其中之一若屬於 P，則其他幾個也屬於 P，其證明方法大都是證明兩個互依問題中間有一個只需要用 O(nk) 時間來完成的橋樑。直到1971年古克 (Stephen A. Cook) 發表了〈The Complexity of Theorem Proving Procedures〉才把 P 之外約問題歸成了三大類，即 NP, NP-complete 及 NP-hard 4 ，現在談古克定律。

发帖者 Alpha 时间： 16:21 0 评论 A A A A

标签： ,

未來數學家的挑戰【二、計算量】

二、計算量

計算量，顧名思意，是指解決某問題所需要計算的時間，但因每個複雜問題的計算往往都要經過許多不同的運算，除加減乘除四則外，還要包含比較，取數據，存數 據等等，若仔細計算起來，十分困難，一般都只繪出一兩個主要的量，加以統計，以上節中售貨員旅行問題為例，其主要的工作是對每一個排法加起總路徑之長，因 對 n 城而言，有 (n-1)! 的排法，我們就定其計算量為 O(n!)，即在 n! 之層次（order 即 O 縮寫之來源）之內。

舉二個例子，我們若要求 n 個數的和或平均值，則其計算量為 O(n)。 但若我們要把 n 個數字依次排列，則其計算量會因做法的不同而有相當的差別，一個直接了當的方法是，先求出最大的（比 (n-1) 次），再從不是最大的中間求次大的（比 (n-2) 次），再求第三大的（比 (n-3) 次），……如此一共比了

\begin{displaymath} (n-1)+(n-2)+\cdots+1\\ =\frac{n(n-1)}{2}\\ \end{displaymath}

次就可以完成此工作。因此我們以 O(n2)，即在 n2 之層次來表此方法的計算量。 另外一種快排法，先把 n 個數分成若干小塊，每塊排好之後再合起來， 則可以證明此種方法之計算量為 $O(n{\log_2{n}})$ 1 ，因排數字與排名字，電話號碼相同，這種排法很有實用價值， 例如某大城有一百萬戶，則 n2=1012，而 $n{\log_2n}$ 只有 2 x 107，其差別三個月與一分鐘之比。

一般計算量的層次多以下表來區分，

\begin{eqnarray*} &&O(\log n)<O(n)<O(n\log_2n)<O(n^2)\\ &&<O(n^k)<O(2^n)<O(k^n)<O(n!) \end{eqnarray*}

在上表中，k 為某一大於 2 的正整數，它們中間都有一道鴻溝，有基本層之不同，在計算機理論上，若某人能發現一個新的方法，降低一個層次的計算量，那麼他的新方法有資格稱之為一個突破，可以不朽矣。表1 有一個對上項各量之比較，是以計算機每秒作一百萬次 (106) 計算為原則。

n $\log n$ n $n\log n$ n2 n3 2n 3n n!
10 10-6 10-5 10-5 10-4 10-3 10-3 0.059 0.45
20 10-6 10-5 10-5 10-4 10-2 1(秒) 58(分) 1年
50 10-5 10-4 10-4 0.0025 0.125 36年 2 x 1010年 1057年
1000 10-5 10-3 10-3 1 16小時 10333年 極大 極大
106 10-5 1 6 1月 105年 極大 極大 極大
109 10-5 16小時 6天 3年 3 x 109年 極大 極大 極大
表一：以計算機每秒做一百萬次時完成各層次計算量所約需的時間（若無單位，均以秒為單位）

在這個表中，特別注意 n3 與 2n 中之差異，一般稱 2n 為計算量呈指數上升，而 n3 或 nk 之計算量呈 n 的方次上升 2 ， 對目前及未來的計算機而言，一個呈方次上升的計算量應可以應付，但對一個呈指數上升的計算量在 n 相當大時則毫無希望。 因此計算機學家所集中精力的方向在如何將一個呈指數上升的計算量問題，簡化成一個方次上升的計算量問題。 我們定義凡對一個問題中最重要的參數 n 而言，若能找到一個方法可以以方次上升的計算量完成， 我們稱此問題為一 P-問題（P 為英文多項式 Polynomial 之第一字母），包含所有此類問題之集合以 P 表示之。

发帖者 Alpha 时间： 16:19 0 评论 A A A A

标签： ,

订阅： 博文 (Atom)